Composite shapes

The basic usage of shapes was explained in the Finite size section of the tutorial. An overview of all the classes and function is available in the Shapes API reference. This section show how multiple of those shapes can be composed to quickly create intricate systems.

Download this page as a Jupyter notebook

Moving shapes

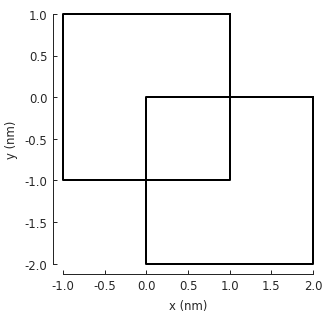
All shapes have a with_offset() method which simply translates the shape by a vector:

shape = pb.rectangle(2, 2)
translated_shape = shape.with_offset([1, -1])
shape.plot()
translated_shape.plot()
../_images/shapes-1.png

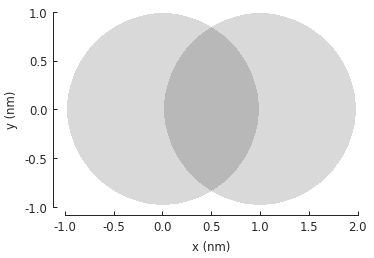
This applies to any kind of shape, including user-defined freeform shapes:

def circle(radius):
    def contains(x, y, z):
        return np.sqrt(x**2 + y**2) < radius
    return pb.FreeformShape(contains, width=[2*radius, 2*radius])

shape = circle(1)
translated_shape = shape.with_offset([1, 0])
shape.plot()
translated_shape.plot()
../_images/shapes-2.png

Note that Polygon and FreeformShape are presented differently in the plots. For polygons, a line which connects all vertices is plotted. Freeform shapes are shown as a lightly shaded silhouette which is filled in by calling the contains function and placing dark pixels at positions where it returned True.

Using set operations

In the examples above we placed 2 shapes so that they overlap, but those were only plots. In order to create a composite shape, we can use logical and arithmetic operator. For example, addition:

s1 = pb.rectangle(2.3, 2.15)
s2 = s1.with_offset([1.12, -1.05])

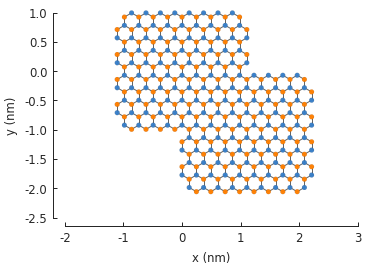
composite_shape = s1 + s2
composite_shape.plot()
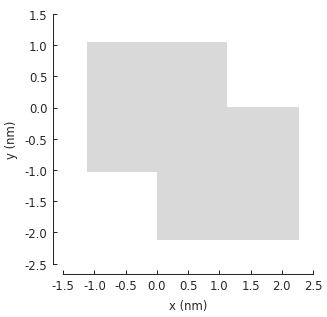
../_images/shapes-3.png

Note that even though we have combined two polygons, the composite shape is plotted in the style of a freeform shape. This is intentional to allow making completely generic shapes.

The + operator creates a union of the two shapes and the result can be used with a model:

from pybinding.repository import graphene

model = pb.Model(graphene.monolayer(), composite_shape)
model.plot()
../_images/shapes-4.png

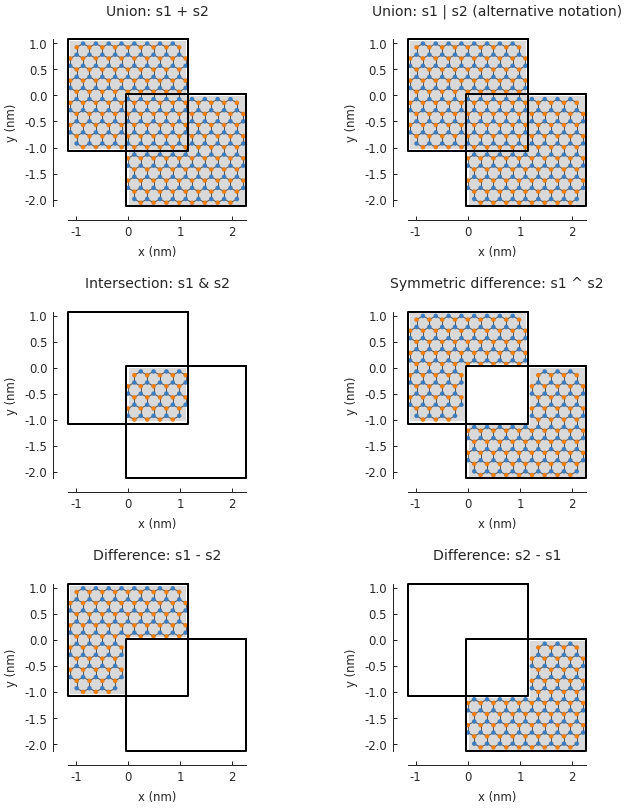
Shapes are composed in terms of set operations (e.g. unions, intersections) and the syntax mirrors that of Python’s builtin set. The available operators and their results are shown in the code and figure below. Note that the + and | operators perform the same function (union). Both are available simply for convenience. Apart from -, all the operators are symmetric.

grid = plt.GridSpec(3, 2, hspace=0.4)
plt.figure(figsize=(6.7, 8))

titles_and_shapes = [
    ("Union: s1 + s2",                          s1 + s2),
    ("Union: s1 | s2 (alternative notation)",   s1 | s2),
    ("Intersection: s1 & s2",                   s1 & s2),
    ("Symmetric difference: s1 ^ s2",           s1 ^ s2),
    ("Difference: s1 - s2",                     s1 - s2),
    ("Difference: s2 - s1",                     s2 - s1)
]

for g, (title, shape) in zip(grid, titles_and_shapes):
    plt.subplot(g, title=title)
    s1.plot()
    s2.plot()
    model = pb.Model(graphene.monolayer(), shape)
    model.shape.plot()
    model.plot()
../_images/shapes-5.png

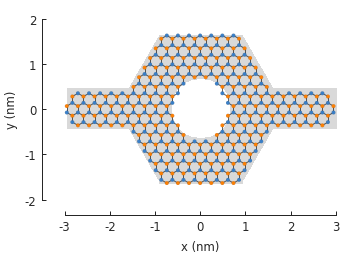
This isn’t limited to just two operands. Any number of shapes can be freely combined:

from math import pi

rectangle = pb.rectangle(x=6, y=1)
hexagon = pb.regular_polygon(num_sides=6, radius=1.92, angle=pi/6)
circle = pb.circle(radius=0.6)

model = pb.Model(
    graphene.monolayer(),
    (rectangle + hexagon) ^ circle
)
model.shape.plot()
model.plot()
../_images/shapes-6.png

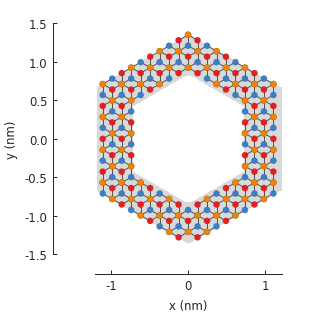
Additional examples

Circular rings are easy to create even with a FreeformShape, but composites make it trivial to create rings as the difference of any two shapes:

outer = pb.regular_polygon(num_sides=6, radius=1.4)
inner = pb.regular_polygon(num_sides=6, radius=0.8)
model = pb.Model(graphene.bilayer(), outer - inner)
model.shape.plot()
model.plot()
../_images/shapes-7.png

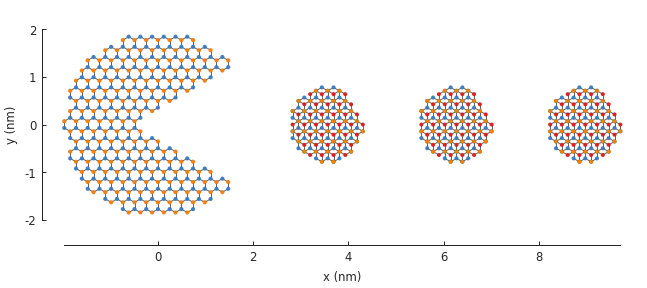
Of course, we can also go a bit wild:

plt.figure(figsize=(6.7, 2.6))

circle = pb.circle(radius=2)
triangle = pb.regular_polygon(num_sides=3, radius=2, angle=pi / 6).with_offset([1.4, 0])
pm = pb.Model(graphene.monolayer(), circle - triangle)
pm.plot()

dot = pb.circle(radius=0.8)
for x in [3.55, 6.25, 8.95]:
    pd = pb.Model(graphene.bilayer(), dot.with_offset([x, 0]))
    pd.plot()
../_images/shapes-8.png