Nanoribbons¶
See the Shape and symmetry tutorial page for more details on nanoribbon construction. These are just a few quick examples.
Bilayer graphene¶
"""Bilayer graphene nanoribbon with zigzag edges"""
import pybinding as pb
import matplotlib.pyplot as plt
from pybinding.repository import graphene
from math import pi, sqrt
pb.pltutils.use_style()
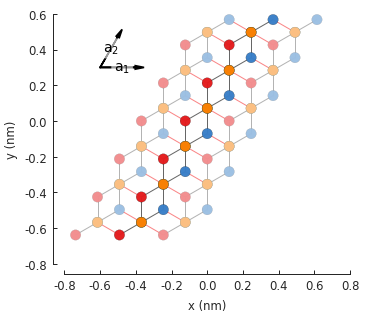
def bilayer_graphene():
"""Bilayer lattice in the AB-stacked form (Bernal-stacked)"""
lat = pb.Lattice(a1=[graphene.a, 0], a2=[0.5*graphene.a, 0.5*sqrt(3)*graphene.a])
c0 = 0.335 # [nm] interlayer spacing
lat.add_sublattices(('A1', [0, -graphene.a_cc/2, 0]),
('B1', [0, graphene.a_cc/2, 0]),
('A2', [0, graphene.a_cc/2, -c0]),
('B2', [0, 3*graphene.a_cc/2, -c0]))
lat.register_hopping_energies({'t': graphene.t, 't_layer': -0.4})
lat.add_hoppings(
# layer 1
([ 0, 0], 'A1', 'B1', 't'),
([ 1, -1], 'A1', 'B1', 't'),
([ 0, -1], 'A1', 'B1', 't'),
# layer 2
([ 0, 0], 'A2', 'B2', 't'),
([ 1, -1], 'A2', 'B2', 't'),
([ 0, -1], 'A2', 'B2', 't'),
# interlayer
([ 0, 0], 'B1', 'A2', 't_layer')
)
lat.min_neighbors = 2
return lat
model = pb.Model(
bilayer_graphene(),
pb.rectangle(1.3), # nm
pb.translational_symmetry(a1=True, a2=False)
)
model.plot()
model.lattice.plot_vectors(position=[-0.6, 0.3]) # nm
plt.show()
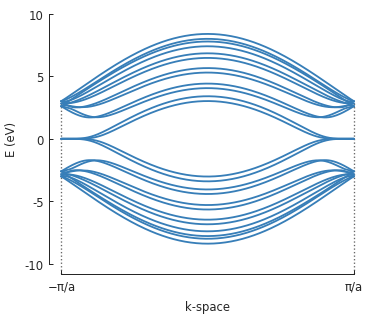
solver = pb.solver.lapack(model)
bands = solver.calc_bands(-pi/graphene.a, pi/graphene.a)
bands.plot(point_labels=[r"$-\pi / a$", r"$\pi / a$"])
plt.show()